PolynomialRegressor: Robust Polynomial Regression with Machine Gnostics

The PolynomialRegressor is a robust polynomial regression model built on the principles of Mathematical Gnostics. It is designed to provide deterministic, interpretable, and resilient regression in the presence of outliers, noise, and non-Gaussian data distributions. Unlike traditional statistical models, this regressor leverages algebraic and geometric concepts from Mathematical Gnostics, focusing on event-level modeling and robust loss minimization.

---

Overview

• Robust to Outliers: Uses gnostic loss functions and adaptive weights to minimize the influence of outliers and corrupted samples.
• Polynomial Feature Expansion: Supports configurable polynomial degrees for flexible modeling.
• Iterative Optimization: Employs iterative fitting with early stopping and convergence checks.
• Custom Gnostic Loss: Minimizes a user-selected gnostic loss ('hi', 'hj', etc.) for event-level robustness.
• Detailed Training History: Optionally records loss, weights, entropy, and gnostic characteristics at each iteration.
• Easy Integration: Compatible with numpy arrays and supports model persistence.

---

Key Features

• Robust regression using gnostic loss functions
• Flexible polynomial degree (linear and higher-order)
• Adaptive sample weighting
• Early stopping and convergence tolerance
• Training history tracking for analysis and visualization
• Handles non-Gaussian noise and outliers
• Compatible with numpy arrays

---

Parameters

Parameter	Type	Default	Description
degree	int	2	Degree of the polynomial to fit.
scale	{'auto', int, float}	'auto'	Scaling method or value for input features.
max_iter	int	100	Maximum number of optimization iterations.
tol	float	1e-3	Tolerance for convergence.
mg_loss	str	'hi'	Gnostic loss function to use ('hi', 'fi', etc.).
early_stopping	bool	True	Whether to stop early if convergence is detected.
verbose	bool	False	If True, prints progress and diagnostics during fitting.
data_form	str	'a'	Internal data representation format.
gnostic_characteristics	bool	True	If True, computes and records gnostic properties (fi, hi, etc.).
history	bool	True	If True, records the optimization history for analysis.
verbose	bool	True	Print detailed progress, warnings, and results
---

Attributes

• coefficients: np.ndarray
  Fitted polynomial regression coefficients.
• weights: np.ndarray
  Final sample weights after robust fitting.
• params: list of dict
  Parameter snapshots (loss, weights, gnostic properties) at each iteration.
• _history: list
  Internal optimization history (if enabled).
• degree, max_iter, tol, mg_loss, early_stopping, verbose, scale, data_form, gnostic_characteristics:
  Configuration parameters as set at initialization.

---

Methods

fit(X, y)

Fits the polynomial regressor to input features X and targets y using robust, gnostic loss minimization. Iteratively optimizes coefficients and sample weights, optionally recording history.

• X: np.ndarray, shape (n_samples, n_features)
  Input features.
• y: np.ndarray, shape (n_samples,)
  Target values.

Returns:
self (fitted model instance)

---

predict(X)

Predicts target values for new input features using the trained model.

• X: np.ndarray, shape (n_samples, n_features)
  Input features for prediction.

Returns:
y_pred: np.ndarray, shape (n_samples,)
Predicted target values.

---

score(X, y, case='i')

Computes the robust (gnostic) R² score for the polynomial regressor model.

• X: np.ndarray, shape (n_samples, n_features)
  Input features for scoring.
• y: np.ndarray, shape (n_samples,)
  True target values.
• case: str, default 'i'
  Specifies the case or variant of the R² score to compute.

Returns:
score: float
Robust R² score of the model on the provided data.

---

save_model(path)

Saves the trained model to disk using joblib.

• path: str
  Directory path to save the model.

---

load_model(path)

Loads a previously saved model from disk.

• path: str
  Directory path where the model is saved.

Returns:
Instance of PolynomialRegressor with loaded parameters.

---

Example Usage

from machinegnostics.models.regression import PolynomialRegressor

# Initialize the model
model = PolynomialRegressor(degree=2, mg_loss='hi', verbose=True)

# Fit the model
model.fit(X_train, y_train)

# Predict
y_pred = model.predict(X_test)

# Score
r2 = model.score(X_test, y_test)
print(f'Robust R2 score: {r2}')

# Access coefficients and weights
print("Coefficients:", model.coefficients)
print("Weights:", model.weights)

---

Training History

If history=True, the model records detailed training history at each iteration, accessible via model.params and model._history. Each entry contains:

• iteration: Iteration number
• loss: Gnostic loss value
• coefficients: Regression coefficients at this iteration
• rentropy: Rentropy value (residual entropy)
• weights: Sample weights at this iteration
• gnostic_characteristics: (if enabled) fi, hi, etc.

This enables in-depth analysis and visualization of the training process.

---

Example Notebooks

• Example 1
• Example 2

---

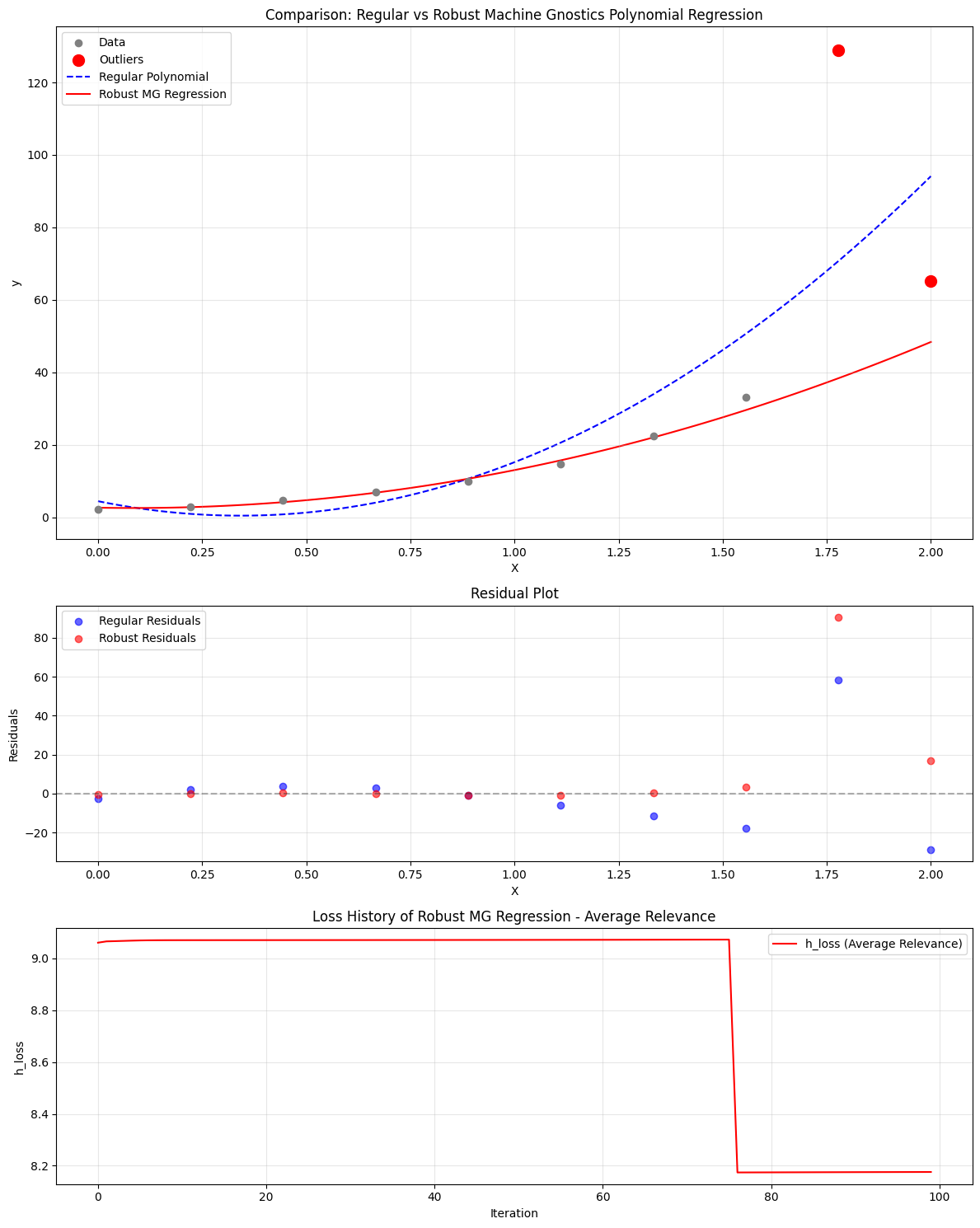
Notes

• The model is robust to outliers and suitable for datasets with non-Gaussian noise.
• Implements advanced machine learning techniques based on Mathematical Gnostics.

---

Author: Nirmal Parmar
Date: 2025-05-01

---